水のかたちにひそむ数学
水道の蛇口からつーっと細く水を落とすと、元の方が太くて先に行くほど細くなって行きます。先日、ふと思いました。これは、水が落ちて行くにつれて重力に引っ張られて、だんだん速くなって行くからじゃないかと。
同じ幅の水では、流れが速いほどたくさんの水が流れます。逆に一定の水が流れている場合には、流れが速くなるとその分、細く流れることになります。人の集団が、ゆっくり道を歩いているときは横に広がってるのに、前の方が走り始めると列が細長くのびちゃうのと似たようなものです。
蛇口から落ちた水も同じでしょう。少し丁寧に言うと<水の速度>×<流れの断面積>=<流量>、流量が一定なら、自由落下で速度が上がるのに反比例して、断面積が減って行くことになります。しかし、この原理で本当にあのきれいに細くなって行く形が生まれるのでしょうか。しばし数学っぽく考えてみました。
ややこしいので細かい事は省略しますが、落下距離は速度の2乗に比例、速度と断面積は反比例、断面積は水の直径の2乗に比例、というような関係をつないで行きます。その結果、水の直径は、蛇口からの距離の-1/4乗で表されると推定しました。
この方法は「次数推定」と言って、そうすることで正確な数値を求めることはできませんが、二つの数字が描く曲線がどんな形になるかだけは想像できます。自然の中の神秘的な形が、どういう仕組みで生まれているのかを考えるには有効な方法です。
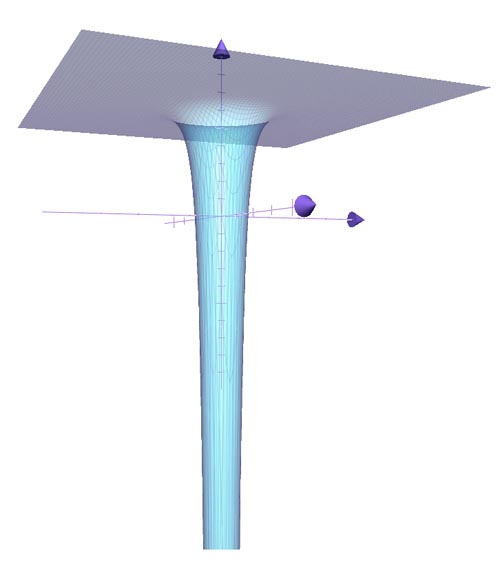
とはいえ、-1/4乗とか言っても全然イメージわきませんよね。その関係を、MacのおまけソフトGrapherで3次元に描いてみたのが上のグラフです。一応なんかそれっぽいものができました。蛇口の先に細くのびる繊細な水の形は、「落下速度に反比例して断面積が小さくなる」という単純な原理から生まれる。という事で良いようです。
私たちがきれいだなーと思う形には、しばしばシンプルな原理が潜んでいます。その形を明快に記述してくれる思考プロセスが数学。無意識の感覚を意識化するためには、数学はとても便利な道具になります。
なお、実際の水道では、途中で水のかたちが崩れてしまうのですが、そのあたりも含めてこの現象を説明した文献をご存じの方、情報をくださるとうれしいです。



筋金入りのMacユーザーの私もGrapherは使ったことがなく。
こんな風に使えるのですね。
数学(私は全くダメですが)も、実生活にあてはめると興味をそそられるものですね!
美しさは自然のものに在り、自然は法則によって成り立っている、
といったことろでしょうか。
Foxの刑事モノのドラマ「Numbers」が人気なのを思い出しました。
この件とはちとズレてますが、数学の面白さという感覚では近いのかな。
適当な憶測ですが、蛇口に近い部分では流速が低いので層流になっていて乱れのない綺麗な流れで、離れるにつれて流速が速くなり、乱流になり乱れた流れになるのではないでしょうか
coさん、おはようございます。
Grapherの存在は学生に教えてもらいました。
サンプルについてくる数式をちょっと弄るだけで、
形が大きく変わるので、結構はまりました。
appleのソフトらしく、意外に表現力があるのがうれしいです。
デザイナーの私が、数学の神秘などを語るのはおこがましくて
このエントリーなども間違ってんじゃないかと、ドキドキです。
しかし、好奇心だけは持ち続けたいと思います。
smbdさん、こんにちは。
そう思います。
この現象のちゃんとした流体力学的解説をwebで探してみたのですが
まだ見つけておりません。
情報がありましたら、教えて下さい。
残念なから文献が見つかりませんが、表面張力(分子間力)による現象だったと記憶しております。
水柱が細くなると空気の揺れ等のチョットした振動で表面に凹凸が出来て凹の部分がより中心の水と引かれ合います。その結果くびれが発生し、やがて水滴になるという感じだったと思います。
振動なくても水は表面張力により球体になりたがるので、より細くなった後に水滴へと変化することに。。。
いつこれを知ったのかも思い出せず裏付けとなる資料もありませんが、文献に行き着くお助けになればと思います。
yagiさん、ありがとうございます。
層流から乱流への変化ではなく、層流のままの分離であるなら、
条件が良ければ非常にきれいな水滴の列になるのかもしれませんね。
大変参考になりました。